To describe the algorithm we define first of all the specialisation of
a mv-rule. Giving a mv-rule and a mv-atom, the mapping 
specialises the mv-rule with respect to that mv-atom generating a
specialised mv-rule, or a new mv-atom if the rule had a single
condition.
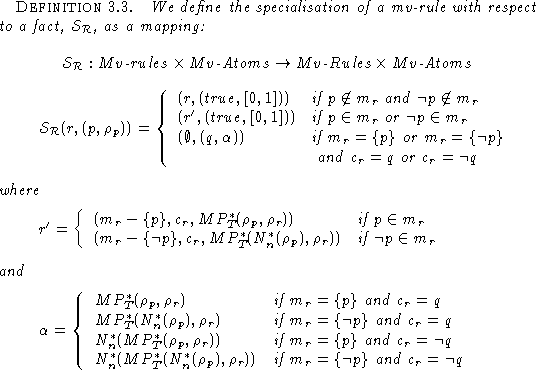
We extend now the definition of specialisation of a mv-rule to that of
the specialisation of a set of rules concluding the same atom p. In
doing so, we select in turn a rule r to specialise. If its
specialisation, with respect to a fact f, returns a new rule, that
is, 
, then we substitute the rule
by the specialised one in the agent's mental state representation, and
the truth-value of p is not changed. If the specialisation returns a
new interval for p, that is, 
,
the rule is eliminated and a new truth-value for p is calculated by
means of the Composition inference rule.
The next definition accounts for the specialisation of an agent's mental state with respect to a set of atoms.
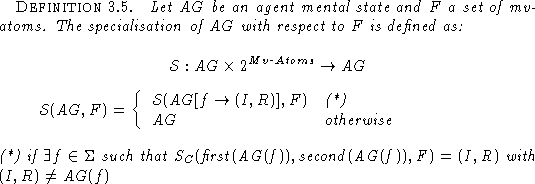
Note: The notation 
represents a modification of the
function AG in such a way that from now on AG(f) = (I,R).
To specialise a complete agent's mental state we will use each atom with definitive value in the mental state in turn to make specialisation steps that possibly will generate definitive values for other atoms to be later on used to specialise more the state. Clearly this process finishes because the number of atoms in any set of rules of the type considered is always finite. Hence the following algorithm
The complexity of this algorithm is 
where 
.